Abstract

A new cosmic model, introduced in 1997, is extended to account for:

1. a vacuum energy, ρ_v ≃ 8.9 × 10⁻³⁰ g-cm⁻³, and Ω_Λ = 8πρ_vG/3H² ≃ 1,
2. the Hubble (m, z) relation,
3. a T(z) = 2.73(1 + z) K relation that fits all current CBR results,
4. the velocity dipole distribution of radiogalaxies,
5. (1 + z)⁻¹ dilation of SNe Ia light curves,
6. the Sunyaev-Zeldovich thermal effect,
7. Olber's paradox,
8. a ~ (1 + z)^−3.56 modified Tolman relation,
9. SN dimming for z < 1, and for z > 1 a brightness enhancement that fits SN 1997ff results, and
10. predicts possible detection of galaxies, quasars, SN and GRBs with z > 10.

Bahcall [1] has enthused "The Big Bang is bang on" because recent Cosmic Blackbody Radiation (CBR) measurements [2] at z = 2.34 match its prediction of 9.1 K. He laments, however, this means he and like-minded colleagues will now miss the excitement of searching for a new cosmic model. His lament is premature. This Letter explores the exciting prospect that the New Redshift Interpretation (NRI), a relatively new cosmic model [3], equally qualifies as being "bang on," first because it accounts for the 2.73 K CBR locally, plus the more recent measurements at z = 2.34 and z = 3.025 [4]. Secondly, because it provides a new explanation of the enhanced brightness of high-z supernovae [5], and the dipole velocity distribution of radiogalaxies [6]. Thirdly, because it makes brightness predictions for even higher redshift (z > 10) objects that strongly suggest they should be detectable. And fourthly because, in a report that has thus far received scant attention [7], I describe what may be a potentially exciting discovery of evidence showing GPS operation reveals the universe is governed relativistically by Einstein's static solution of the field equations, with its fixed in-flight photon wavelength (λ) prediction, and not big bang's Friedmann-Lemaitre (F-L) solution, with its hypothesized in-flight λ variation and cosmological redshifts. Unless this discovery is refuted, then: (i) It follows that cosmological redshifts — upon which all of big bang is hinged — are not genuine physical phenomena and, (ii) an alternative astrophysical framework of the cosmos must exist that incorporates the Einstein static solution with its fixed in-flight λ, along with radically different initial conditions. This Letter extends the NRI model as a first step in formulating a new cosmic model.

In late 1997, before the SNe Ia evidence for cosmic repulsion was published in early 1998 by Riess et al. [8] and Perlmutter et al. [9], I developed the NRI model [3], which predicted that ours is a universe dominated by vacuum energy density, ρ_v ≃ 8.9 × 10⁻³⁰ g-cm⁻³ and density parameter (Ω_Λ)_NRI = 8πρ_vG/3H_o² ≃ 1,which compares to Ω_Λ ~ 0.7 from SNe Ia observations [5]. The NRI accounts for the Hubble redshift relation in terms of Einstein gravitational redshifts and relativistic Doppler redshift caused by vacuum gravity repulsion. Since the latter produces a true Hubble recession of the galaxies away from a nearby cosmic Center (C), the NRI represents a physically expanding universe, but without big bang's singularity, F-L expansion, and Cosmological Principle. In particular the NRI associates the 2.7 K CBR with cavity radiation, instead of expansion-shifted big bang relic radiation. Cavity radiation exists in the NRI model because in it galaxies of the visible universe are enclosed by a thin, very distant outer shell of closely spaced galaxies at a distance R from C. The concept of a nearby C departs radically from modern cosmology, but it uniquely accounts for the existence of both the heretofore unexplained quantized redshifts and quasar redshift peaks [10]. This Letter contends that quasars grouped in different z_i ± ∆z_i intervals are in different spherical shells at cosmological distances — hence that a Center exists nearby — thus implying that Earth's motion through the CBR must result in a dipole velocity distribution of distant galaxies. This has now been confirmed [6].

The NRI's explanation of the CBR's temperature measurements utilizes the radial variation of gravitational potential within the spherical cavity. Thus blackbody cavity radiation temperature, T(z), at any interior point, P, depends on the Einstein gravitational redshift between P and the outer shell, or between P and C. In fact if the vacuum pressure, p_v, is negative, then the vacuum density, ρ_v, will be positive, and the summed vacuum pressure/energy contributions to vacuum gravity will be −2ρ_v. So, excluding the outer galactic shell at R, the net density throughout the cosmos from C to R would be ρ − 2ρ_v, where ρ is the average mass/energy density of ordinary matter. Beyond R both densities are assumed to either cancel or diminish to negligible values, which effectively achieves for the NRI framework what Birkhoff's theorem did for standard cosmology. By including ρ_v and p_v into the gravitational structure of the cosmos, together with appropriate boundary conditions, one obtains T(z) = 2.73(1 + z) K for the CBR temperature redshift equation [3], which duplicates big bang's prediction for all z, but without its F-L expansion. Thus, radiation emitted from the outer shell is gravitationally redshifted to become the 2.73 K blackbody cavity radiation here at the Galaxy [3], and 9.1 K at z = 2.34 and 10.97 K at z = 3.025, in accord with recent measurements of 6.0 K < T < 14 K [2] and T = 12.1_−3.2^+1.7 K [4]. Interestingly, years ago Misner et al. [11] theorized, "The cosmic microwave radiation has just the form one would expect if the earth were enclosed in a box ('blackbody cavity') with temperature 2.7 K." The MTW box resembles the NRI's outer shell. But the NRI's vacuum energy and gravitational redshifts clearly distinguish it from the MTW scenario.

True blackbody cavity radiation results from assuming the outer shell consists of regularly spaced galactic clusters with stars composed of pure H at uniform temperature 5400 K, which, within broad limits, is an adjustable parameter [3]. On this basis the gravitational redshift from the outer shell to C is 5400 K/2.726 K ≃ 2000, and the distance from C to the outer shell is R = 14.24 × 10⁹ ly [3]. Thus in the NRI the ripples in the CBR [12, 13] are preliminarily attributed to either regularly spaced voids between its galactic clusters and/or small temperature variations within the clusters. A separate paper [14] explores whether the latter might also account for the thus far unexplained hot spots in the 2.7 K CBR [15]. Moreover since all galaxies in the visible universe are backlighted by the outer shell, they will cast a shadow in local 2.7 K CBR measurements. This is a new interpretation of the Sunyaev-Zeldovich (S-Z) thermal effect [16]. The kinematic S-Z effect is treated separately [14].

To compare the NRI model with the Tolman relation we follow the treatment of Ellis [17] and let L be a galaxy's intrinsic luminosity, and r_g, the galaxy observer distance measured by an observer in the galaxy's rest-frame. The proper flux measured locally would be F_g = L/4πr_g². However, NRI's redshift expression [3] contains r, the observer area distance, which is the galaxy's quasi-Euclidean distance as measured by a stationary local observer [17]. Aberration gives rise to a reciprocity relation between distance measures [17] such that r_g = r (1 + z_d), where 1 + z_d is the NRI's special relativistic Doppler redshift factor, and v is the galactic recessional velocity relative to a fixed local observer [3]. Thus photons arrive locally by a factor of (1 + z)⁻¹ slower than emitted in the receding rest frame due to the combined relativistic Doppler and gravitational redshifts. This relative clock rate slowing accounts for the (1 + z)⁻¹ broadening of SNe Ia light curves [18, 19]. Additionally, each photon arriving locally will likewise have its energy diminished by this same redshift factor. Thus the flux, F, measured by a local observer would be

after utilizing the r_g = r (1 + z_d) substitution. If only Doppler effects are operational then, as Misner et al. [11] show, the flux is F_dopp = L(1 + z_d)⁻⁴ / 4πr² and the bolometricintensity is I_dopp = F/∆Ω = I_o(1 + z_d)⁻⁴, where ∆Ω is the solid angle subtended by the source at r [17]. By analogy, for the NRI we find

Utilizing the NRI's total redshift factor [3], 1 + z = (1 + Hr/c) / √1 − 2(Hr/c)², along with its Doppler factor, 1 + z_d = (1 + Hr/c) / √1 − (Hr/c)², allows fitting I solely in terms of z over the interval, 0 < z < 1, namely,

which differs from the Tolman relation, I_bb = I_o / (1 + z)⁴. Interestingly, Lubin et al. [20], in reporting observations on 34 galaxies from three clusters with z = 0.76, z = 0.90, and z = 0.92, conclude the exponent on (1 + z) varies from 2.28 to 2.81 in the R band, and 3.06 to 3.55 in the I band, depending on q_o's value. Further study is needed to assess the significance of the I band's near agreement with the NRI result. Of course Lubin and Sandage were unaware of this possible connection with the NRI model.

Instead they propose evolutionary effects could bring their results in agreement with the Tolman exponent, n = 4, which they assume is correct using the usual argument that no deviation in the CBR has been found to one part in 10⁴ [21]. In fact, however, this argument is flawed. The problem begins with Lubin and Sandage's assumption that the CBR is big bang's relic radiation, on which basis they conclude that an initial blackbody spectrum would remain Planckian only if the normalization is decreased with redshift by (1 + z)⁻⁴. They then reason that, since the Planck equation defines a surface brightness, a test of the Tolman surface brightness is obtainable from measuring the deviation of the photon number per unit surface area of the sky by comparing observations with the normalization given by the Planck equation. They then say, correctly, that no deviation in the CBR has been found to one part in 10⁴. Then, because they assume the CBR is big bang relic radiation, they conclude it must have experienced perfect normalization due to cosmic wavelength expansion, which in turn implies validity of the Tolman surface brightness factor.

This Letter challenges their association of the CBR with big bang relic radiation, first because Ref. 7 calls expansion redshifts into question, and second because the NRI model provides an alternative explanation that has nothing to do with cosmic expansion and its prediction of the Tolman factor. What we have is a failure to distinguish between necessary and sufficient conditions. That is, while it is true that the CBR is Planckian to a high degree of precision, this is only a necessary condition for it to be identified with big bang's relic radiation, not a sufficient condition. Indeed, the assumption that the NRI's outer shell's galactic clusters are composed of pure H stars — which are assumed to have originated in a different epoch than those in the visible universe — also guarantees that the CBR must be Planckian to an equally high degree of precision in the NRI model.

Turning attention now to the NRI's (m, z) relation, using Eq. (1) we utilize the usual definition for the luminosity distance and write
d_L = √L / 4πF = r_g(1 + z) = r(1 + z)(1 + z_d), which becomes d_L = r(1 + z)² for z < 1. In this interval the NRI's (1 + z) redshift factor is approximated by Hr/c ≈ z/(1 + z), which leads to d_L = cz(1 + z)/H. Substituting into the distance modulus, m − M = 5(logd_L − 1), we find

as a reasonable fit over 0 < z < 1, which compares closely with standard cosmology's redshift prediction,

for the recent estimate of q_o ≈ −0.75 [18]. If we write ℳ = M − 5[logH − log(1 + z)] − 5, then Eq. (4) reduces to m = ℳ + 5 log cz, the Hubble relation for z ≪ 1.

To investigate the expected brightness for z > 1 we adapt other parts of the analysis of Ellis [17] to obtain the specific intensity, i_v = F_v /∆Ω, the specific flux per unit solid angle, for the NRI model. Let the source spectrum be represented by a function φ(v_g), where Lφ(v_g) is the rate at which radiation is emitted from the galaxy at frequencies between v_g and v_g + dv_g, with φ(v_g) normalized so that ∫₀^∞φ(v_g)dv_g = 1. The frequency, v, measured by some stationary observer at r is related to the emission frequency, v_g, in the galaxy's rest frame by v = v_g / (1 + z), which implies dv = dv_g / (1 + z). Following the treatment of Ellis [17] the flux expression becomes

Defining the specific flux over the interval dv as Ref. 17, F_vdv = Lφ(v)dv/(4πr²(1 + z)(1 + z_d)², we obtain, after substitutions, the specific flux, F_v = F_gφ(v)/r²(1 + z)(1 + z_d) ², from which it follows that

iv   =     Fv ΔΩ   Fgφ(v) / A (1 + z)(1 + zd)2     =    Igφ (v) (1 + z)(1 + zd)2  ,

(7)

where A is the surface area of the source and I_gφ(v) = i_o is the surface brightness of the source at frequency v (see Ellis [17], p. 163). In the NRI (1 + z) ≈ (1 + z_d) for z < 1, in which case (i_v / i_o) _NRI ≈ (1 + z)⁻³ for this redshift interval, the same as big bang's prediction of (i_v / i_o)_bb = (1 + z)⁻³. But for higher redshifts 1 + z ≠ 1 + z_d, in which case we must use the full expression,

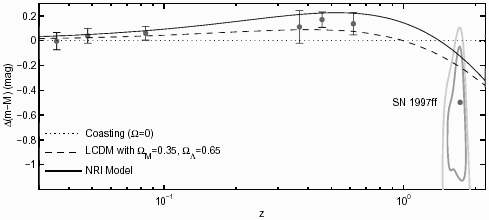
Before showing how Eq. (8) accounts for the apparent luminosity of some high-z galaxies, we turn attention to the NRI model's prediction of SN Ia brightness enhancement. Fig. 11 of Riess et al. [5] compares predictions of several cosmological models with data obtained from the High-z Supernova Search team (Riess et al. [8]), the Supernova Cosmology Project (Perlmutter et al. [22]), and their own observations of SN 1997ff. Fig. 1 in this Letter reproduces (with Riess' permission) Fig. 11's redshift data, including its point at z = 1.7 for SN 1997ff, along with the favored LCDM distance modulus curve, as well as Riess et al.'s 68% and 95% confidence contours for the SN 1997ff modulus. Additionally, Fig. 1 also includes an equivalent plot of ∆(m − M)_NRI. The protocol used for obtaining ∆(m − M)_NRI was the same as for that used in Fig. 11, which means that the value of ∆(m − M)_NRI was computed by comparison against the Coasting (Ω = 0) model. Thus, ∆(m − M)_NRI = 5 log d_L / D_L , where d_L is defined above, and D_L is defined by Riess et al. [8]). It can be seen that at z = 1.7 the NRI produces an enhanced brightness relative to the Coasting model of 0.1 magnitudes compared to the LCDM enhancement of 0.2 magnitudes. This puts the NRI's prediction within the 68% contour for the SN 1997ff distance modulus. Additionally, the proper NRI distance modulus traces the LCDM modulus quite well (within the error bars) over the redshift interval 0 < z < 2.

FIG. 1: Hubble diagram of SNe Ia minus an "empty" (Ω = 0) Universe compared to the LCDM model and the equivalent NRI model. This graph partially reproduces Fig. 11 of Riess et al. [8]. The points are the redshift-binned data from the HZT (Riess et al. [8]) and the SCP (Perlmutter et al. [22]). Confidence intervals of 68% and 95% for SN 1997ff are indicated.

Returning now to apparent ultraluminosity of high-z galaxies, Disney [23] recognizes it is extraordinary that galaxies at z = 2 are observed at all given that their apparent brightness is reduced by the Tolman factor, in this instance (1 + z)⁻⁴ ~ 10⁻². Consider further the high redshift z = 5.74 galaxy [24], which was primarily visible and its redshift possible due to very strong Lyman alpha emission. Here the Tolman factor is ~ 5 × 10⁻⁴. The problem in observing high-z galaxies in the standard cosmology is lessened by comparing big bang's heterochromatic dimming factor, (1 + z)⁻³, in comparison with the NRI's, as given in Eq. (8). The latter diminishes more slowly as r increases because 1 + z_d increases more slowly than does the NRI's combined gravitational and Doppler factor, 1 + z. For z = 5.74 big bang's dimming factor is (1 + z)⁻³ ≈ 0.003, whereas the NRI dimming factor from Eq. (8) is (1 + z)⁻¹ (1 + z_d)⁻² ≈ [(6.74)(1.9)(1.9)]⁻¹ ≈ 0.04. The more recent observation of Hu et al. [25] of a galaxy at z = 6.56 yields ≈ 0.01 for the bb and ≈ 0.15 for the NRI, assuming a 4.5 magnification [25]. The quasars at z = 5.82, 5.99 and 6.28 [26] yield greater differences without magnification. Consider also the photometric redshift determination of Yahata et al. [27] of 335 faint objects in the HDF-S, which has tentatively identified eight galaxies with z > 10, two with z ~ 14 and one with z ~ 15. If confirmed these redshifts require standard dimming factors stretching from (1 + z)⁻³ ≈ 1/1300 to 1/4000, whereas the NRI model yields (1 + z)⁻¹(1 + z_d)⁻² ≈ 1/60 and 1/90 for z = 10 and 15 respectively. Also of interest are the observations by Totani et al. [28] of Hyper Extremely Red Objects. These they primarily associate with primordial dust-reddened galaxies at z ~ 3, while also admitting they may instead be galaxies with z ≳ 10. Such are unexpected with the standard cosmology, but they are explainable within the NRI model. Moreover, even though Eq. (8) yields an enhanced apparent brightness compared to the standard cosmology, it still accounts for Olber's paradox because the NRI model represents a bounded universe, and hence a diminishing number density of high-z galaxies.

At even higher z the differences between the NRI and big bang are more significant. In the big bang celestial objects do not even exist at z > 100, or even z > 50. But the NRI model has no such constraints. As its 1 + z = (1 + Hr/c) / √1 − 2(Hr/c)² relation reveals, z increases without limit as r → c /√2H. Thus, astronomers searching for very high redshift galaxies, quasars, SN, and GRBs should be alert to the NRI's prediction of objects with z > 10. The exotic AGN sources detected by Chandra [29], some possibly with z > 6, fit this scenario. Moreover, since the NRI has no constraints on the number density of primordial black holes, it allows certain types of GRBs to originate from these sources [30].

References

1. J. Bahcall, Nature 408, 916 (2000).
2. R. Srianand, P. Pettijean, and C. Ledoux, Nature 408, 931 (2000).
3. R.V. Gentry, Mod. Phys. Lett. A 12, 2919 (1997).
4. S.A. Levshakov et al., astro-ph/0201043.
5. A.G. Riess et al., Astrophys. J. 560, 49 (2001).
6. Chris Blake and Jasper Wall, Nature 416, 150 (2002).
7. R.V. Gentry and D.W. Gentry, gr-qc/9806061.
8. A.G. Riess et al., Astron. J. 116, 1009 (1998).
9. S. Perlmutter et al., Nature 391, 51 (1998); Astrophys. J. 517, 565 (1999); astro-ph/9812473.
10. G. Burbidge andW.M. Napier, Astron. J. 121, 21 (2001).
11. C.W. Misner, K.S. Thorne, and J.A. Wheeler, Gravitation (W.H. Freeman & Co., 1973), pp. 712, 783, 794.
12. P. de Bernardis et al., Astrophys. J. 564, 559 (2002).
13. A.T. Lee et al., Astrophys. J. 561, L1 (2001).
14. R.V. Gentry, in preparation.
15. M.S. Kowitt et al., Astrophys. J. 482, 17 (1997).
16. L. Grego et al., Astrophys. J. 539, 39 (2000).
17. G.F.R. Ellis in General Relativity and Cosmology, edited by R.K. Sachs (Academic Press, 1971), p. 144.
18. A.V. Filippenko and A.G. Riess, astro-ph/0008057.
19. G. Goldhaber et al., in Thermonuclear Supernovae, edited by P. Ruiz-Lapuente et al. (Kluwer, 1997), p. 777.
20. L.M. Lubin and A. Sandage, Astron. J. 122, 1084 (2001).
21. D.J. Fixsen et al., Astrophys. J. 473, 576 (1996).
22. S. Perlmutter et al., Astrophys. J. 517, 565 (1999).
23. M. Disney, Gen. Rel. Grav. 32, 1125 (2000).
24. E.M. Hu and R.G. McMahon, Astrophys. J. 522, L9 (1999).
25. E.M. Hu et al. astro-ph/0203091.
26. ] R.H. Becker et al., Astron. J. 122, 2850 (2001).
27. N. Yahata et al., Astrophys. J. 538, 493 (2000).
28. T. Totani et al., Astrophys. J. 558, L87 (2001).
29. D.M. Alexander et al., astro-ph/0202044.
30. D.B. Cline, C. Matthey, and S. Otwinowski, astroph/ 0110276.